堆積排序 Heapsort
Heapsort(堆積排序)可以看作是 selection sort 的變形,同樣會將資料分為 sorted pile 與 unsorted pile,並在 unsorted pile 中尋找最大值(或最小值),加入 sorted pile 中。
和 selection sort 不同之處是,heapsort 利用堆積(heap)這種半排序(partially sorted)的資料結構輔助並加速排序。
Heapsort 的特性如下:
- 使用 heap 資料結構輔助,通常使用 binary heap。
- 不穩定排序:排序後,相同鍵值的元素相對位置可能改變。
- 原地排序:不需額外花費儲存空間來排序。
- 較差的 CPU 快取:heap 不連續存取位址的特性,不利於 CPU 快取。
步驟
Heapsort 的演算法分為兩大步驟:
- 將資料轉換為 heap 資料結構(遞增排序用 max-heap, 遞減排序選擇 min-heap)。
- 逐步取出最大/最小值,並與最後一個元素置換。具體步驟如下:
- 交換 heap 的 root 與最後一個 node,縮小 heap 的範圍(排序一筆資料,故 heap 長度 -1)。
- 更新剩下的資料,使其滿足 heap 的特性,稱為 heap ordering property。
- 重複前兩個步驟,直到 heap 中剩最後一個未排序的資料。
透過 GIF 動畫感受一下 heapsort 的威力吧!

說明
在開始之前,定義幾個 heap 常用名詞:
- Heap ordering property:一個 heap 必須要滿足的條件。以 heap 種類不同有幾種變形。
- min-heap property:每個結點皆大於等於其父節點的值,且最小值在 heap root。
- max-heap property:每個結點皆小於等於其父節點的值,且最大值在 heap root。
而 heapsort 主要分為兩個部分:
- Heapify:將陣列轉換為 heap 資料結構(heapify)。
- Sorting:不斷置換 heap root 與最後一個元素來排序,並修正剩餘未排序資料使其符合 heap order。
這裡有一個未排序的序列,將以遞增方向排序之。
[17, 20, 2, 1, 3, 21]
首先,將資料轉換為 heap 資料結構,這個步驟即時 heapify。由於是遞增排序,我們採用 max-heap(最大元素在 root)。
[21, 20, 17, 1, 3, 2]
對應的二元樹(binary tree)的圖形如下:
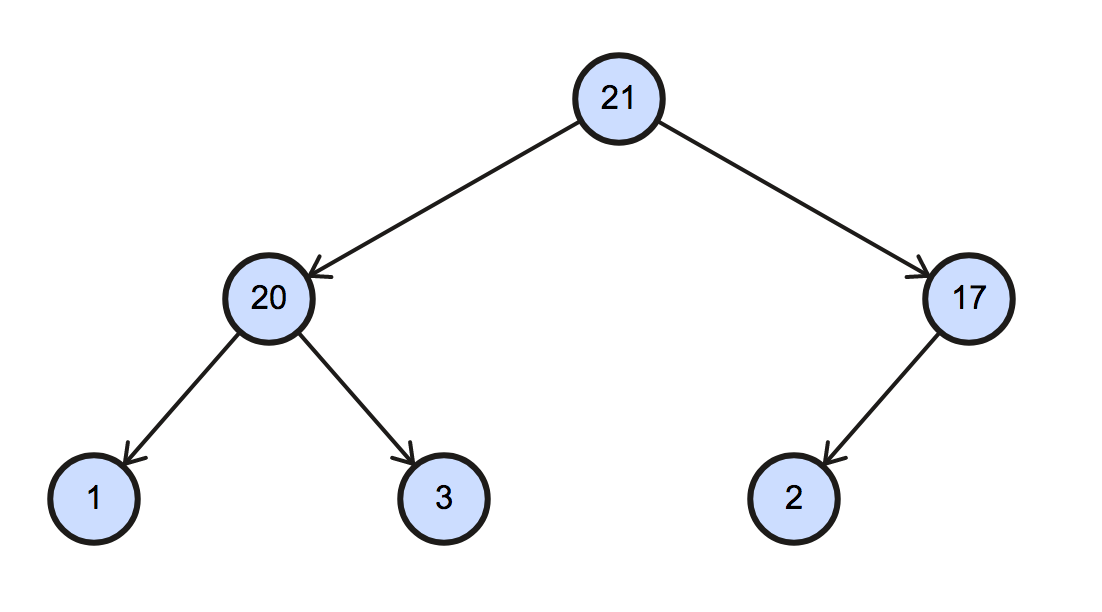
再來就是排序的部分,Max-heap 會將最大的元素擺在 root 的位置,我們先將最後一個 node 與 root 進行交換,完成第一個排序步驟。
若不熟悉 heap,可以閱讀 Wiki 的介紹,其實 heap 就是用陣列實作的二元樹。
[21, 20, 17, 1, 3, 2]
* *
(swap) -->
unsorted | sorted
[2, 20, 17, 1, 3 | 21]
接下來,將未排序的資料區塊重整為符合 max-heap 的結構。
[2, 20, 17, 1, 3 | 21]
(sift down) -->
[20, 3, 17, 1, 2 | 21]
有沒有看出一些端倪?
只要不斷將 root 和最後一個 node 交換,並將剩餘資料修正至滿足 heap ordering,就完成排序了。
[20, 3, 17, 1, 2 | 21]
* *
(swap) -->
[2, 3, 17, 1 | 20, 21]
(sift down)-->
[17, 3, 2, 1 | 20, 21]
* *
(swap) -->
[1, 3, 2 | 17, 20, 21]
(sift down)-->
[3, 1, 2 | 17, 20, 21]
* *
(swap) -->
[1, 2 | 3, 17, 20, 21]
(Done!)
以上便是 heapsort 演算法的簡單流程,是不是和 selection sort 非常相似呢!
效能
| Complexity | |
|---|---|
| Worst | $O(n \log n) $ |
| Best | $O(n \log n) $ |
| Average | $O(n \log n) $ |
| Worst space | $O(1) $ auxiliary |
Heapsort 最佳、最差、平均的時間複雜度皆為 $O(n \log n) $,同樣分為兩部分簡單解釋。
Build heap (heapify)
建立一個 binary heap 有兩種方法,一種是一個個元素慢慢加入 heap 來建立;另一種則是給定隨意的序列,再透過 heapify 演算法修正序列為有效的 heap。一般來說 heapsort 常用實作後者。
Heapify 是指將序列修正至符合 heap ordering 的序列。給定一個元素,假定其為非法的 heap order,而該元素之後的 subtree 視為符合 heap ordering property。欲修正這個在錯誤位置的元素,必須透過與其 children node 置換往下篩,這個往下篩的過程就稱為 sift down,在實作一節會詳細解釋,這邊只要知道 sift down 會不斷將該元素與其 child node 比較,若不符合 heap order 則與 child node 置換,並繼續疊代每一個 level。所以 sift down 的時間複雜度為 $O(\lceil {\log_2(n)} \rceil) = O(\log n) $, $n $ 為陣列元素個數。
Heapify 從最末個元素開始反向疊代,每個元素都呼叫 sift_down 調整 heap 符合 heap ordering。總共要做 $n $ 次 sift_down 操作,但由於最後一層所以 leaf 已符合 heap order(因為沒有 child node),我們的迴圈可以跳過所有 leaf node 直接從非 leaf node 開始,因此複雜度為
$$\lfloor n / 2 \rfloor \cdot O(\log n) = O(n \log n)$$
實際上,build heap 步驟的複雜度可達到 $O(n) $,可以看看 UMD 演算法課程 Lecture note 的分析。
Sorting (sift down)
講完了 heapify,就換到排序部分,所謂的排序其實就是利用 max-heap(或 min-heap)的最大值(最小值)會在首個元素的特性,與最後一個元素置換,完成排序,並將剩餘的部分透過 sift down 修正符合 heap order。所以總共需要做 $n $ 次 sift down,複雜度為 $O(n \log n) $。
Sum up
綜合這兩部分,可以看出 Sorting part 對複雜度有決定性影響,最佳複雜度為 $O(n \log n) $。
實作
Heapsort 的實作相對簡單,只需要不斷呼叫 heap 內部的 sift_down 方法就可以完成排序。整個演算法架構如下:
#![allow(unused)] fn main() { pub fn heapsort(arr: &mut [i32]) { // -- Heapify part -- // This procedure would build a valid max-heap. // (or min-heap for sorting descendantly) let end = arr.len(); for start in (0..end / 2).rev() { // 1 sift_down(arr, start, end - 1); } // -- Sorting part -- // Iteratively sift down unsorted part (the heap). for end in (1..arr.len()).rev() { // 2 arr.swap(end, 0); // 3 sift_down(arr, 0, end - 1); // 4 } } }
- 這部分是 heapify,從最小 non-leaf node 開始(
end/ 2),修正序列至滿足 heap order,再反向疊代做 heapify。 - 這部分負責排序,每次疊代都將排序 heap 的 root 元素,步驟如 3 - 4:
- 不斷將 max-heap 中最大值(在 root 上)與 heap 最後一個元素
end置換, - 並利用
sift_down將序列修正至 max-heap 資料結構,依照定義,此時 unsorted pile 首個元素成為 max-heap root,是最大值。
Heapsort 全靠 sift_down 神救援,那 sift_down 到底有什麼神奇魔力,一探究竟吧!
#![allow(unused)] fn main() { fn sift_down(arr: &mut [i32], start: usize, end: usize) { let mut root = start; loop { let mut child = root * 2 + 1; // Get the left child // 1 if child > end { break; } if child + 1 <= end && arr[child] < arr[child + 1] { // 2 // Right child exists and is greater. child += 1; } if arr[root] < arr[child] { // 3 // If child is greater than root, swap'em! arr.swap(root, child); root = child; } else { break; } } } }
sift_down 的功能是將 node 往下移。通常用在 heap 刪除或取代 node 時,將序列修正為有效的 heap。 這裡實作的版本有三個參數:
arr:欲修正為符合 heap 定義的序列。start:欲往下移動的 node index,可視為需要被修正的元素。end:此 node 以內(包含)的序列都會被修正為有效的 heap。
sift_down 有些假設條件:從 start index 出發的子樹,除了 start 本身以外,其他皆符合 heap ordering。
再來看看 sift_down 實作內容,loop 中幹的活就是不斷將 start index 上的元素與其子樹比較,若不符合 heap ordering,則兩者置換。
- 是否有子結點:依照 binary heap 的定義找出 root 的左子樹(left substree),若左子樹的 index
child比end還大,表示沒有 heap 沒有子結點,停止疊代。 - 檢查右子樹值較大:若 root 下有右子樹且較大,我們會標記右子樹,並在下一步對右子樹進行處理。
- 置換:若
root元素比child的元素小,則置換兩者,並將child設置為下個疊代的root,繼續檢查最初的start元素是否滿足 heap ordering。
以上就是簡單的 sift_down 實作,也是整個 heapsort 的精髓。
參考資料
- Wiki: Heap
- Wiki: Heapsort
- CMSC 351 Algorithms, Fall, 2011, University of Maryland.
- Sorting GIF by RolandH CC BY-SA-3.0 via Wikimedia Commons.