插入排序 Insertion Sort

Insertion sort 是最簡單的排序法之一，比起 quicksort 等高效的排序法，對大資料的處理效能較不理想。其演算法是將欲排序元素直接插入正確位置，因而得名。

Insertion sort 基本特性如下：

實作簡單易理解。
資料量少時較高效，且比其他 $O(n^2) $ 的排序法高效（selection sort/bubble sort）。
自適應排序：可根據當前資料排序情形加速排序，資料越接近排序完成，效率越高。
穩定排序：相同鍵值的元素，排序後相對位置不改變。
原地排序：不需額外花費儲存空間來排序。
即時演算法：可處理逐步輸入的資料，不需等資料完全備妥。

步驟

將序列分為未排序與部分排序兩個區域。

取第一個元素，將該元素視為已排序。
取出下一元素，該元素將插入序列的部分排序區域。
尋找正確位置：若部分排序元素比新元素大，則互換位置。並重複步驟 2 - 3，直到部分排序元素小於等於新元素。
插入元素：將新元素插入最後的位置。
重複步驟 2 - 4，直到排序完成。

簡而言之，即是每次取一個元素，尋找並插入該元素在部分排序區域的排序位置，再逐步把序列單邊排序完成。

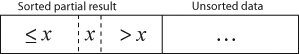
Insertion sort 非常簡單，看動畫就能明瞭。

效能

	Complexity
Worst	$O(n^2) $
Best	$O(n) $
Average	$O(n^2) $
Worst space	$O(1) $ auxiliary

最佳時間複雜度發生在資料已完成排序的狀況下，insertion sort 只需執行最外層的迴圈 $n $ 次。

最差時間複雜度發生在資料完全相反時，insertion sort 每取得一個新元素是，都需將資料插入序列最前面，，因此所需的操作如下（ $c $ 為任意常數）：

$$ c \cdot 1 + c \cdot 2 + c \cdot 3 \cdots + c \cdot (n - 1) = \frac{c(n - 1 + 1)(n - 1)}{2}$$

最後等於

$$\frac{cn^2}{2} - \frac{cn}{2}$$

捨去低次項，得到時間複雜度為 $O(n^2) $。

實作

簡單實作的程式碼如下：


#![allow(unused)]
fn main() {
pub fn insertion_sort(arr: &mut [i32]) {
    for i in 1..arr.len() {                   // 1
        let mut j = i;
        while j > 0 && arr[j - 1] > arr[j] {  // 2
            arr.swap(j - 1, j);
            j -= 1;
        }
    }
}
}

外層迴圈疊代整個序列。並取出 index i，arr[i] 是待排序的元素，index 比 i 小的元素則組成已排序的部分序列。
內層迴圈負責元素比較，決定待排序元素該從何處插入，若前一個元素比待排元素大，則置換兩元素，並繼續往下尋找正確的插入點。直到 j == 0 或待排元素比任何已排序元素都大為止。

變形

Binary Insertion Sort

在一般演算法討論中，通常以簡單的型別如 i32 來探討並實作。在真實世界中，做哪種操作，用哪種語言，都會影響到實際效能。例如 Python 的比較操作相對於置換元素，成本高出不少，是因為每個物件在 Python 的比較需動態檢查是否實作 __lt__ __gt__ 等方法才能進行比較。所以 Python 排序法實作就要特別注意減少比較操作的次數。

Binary insertion sort 的目的就是減少內層迴圈的比較次數。在內層迴圈開始之前，使用 binary search 搜尋新元素應要插入哪個位置，最多僅需 $\log_2n $ 次比較。但 binary insertion sort 的複雜度依舊是 $O(n^2) $，因為除了比較之外，仍需置換（swap）、賦值（assign）等基礎操作。

Binary insertion sort 的程式碼和一般的 insertion sort 差不了多少，我們這裡使用 slice 內建的 binary_search 來找尋插入點。


#![allow(unused)]
fn main() {
pub fn binary_insertion_sort(arr: &mut [i32]) {
    for i in 1..arr.len() {
        let val = arr[i];
        let mut j = i;
        let pos = match arr[..i].binary_search(&val) { // 1
            Ok(pos) => pos,                            // 2
            Err(pos) => pos,
        };
        while j > pos {                                // 3
            arr.swap(j - 1, j);
            j -= 1;
        }
    }
}
}

先限制 binary_search 範圍，取出 sorted pile arr[..i]。再對 slice 執行 binary_search。
binary_search 回傳一個 Result<usize, usize> 型別，找到時回傳 Ok(index 值)，找無時回傳 Err(不影響排序穩定度的插入點)，這個 Err 的設計巧妙解決新值插入的問題。
和普通 insertion sort 雷同，從插入點至 sorted pile 疊代到末端以進行排序，省下不少比較操作。

參考資料

Wiki: Insertion sort
CPython: listsort note
Sorting GIF by Swfung8 (Own work) CC BY-SA 3.0 via Wikimedia Commons.

Rust Algorithm Club

插入排序 Insertion Sort

步驟

效能

實作

變形

Binary Insertion Sort

參考資料